Schon seit vielen Jahren kümmere ich mich um die EDV in unserer Bücherei [1] und ebenfalls seit vielen Jahren sind die Medien in unserer Bücherei mit einem Barcode gekennzeichnet und katalogisiert.
Ein handelsüblicher Barcode-Scanner kann die Barcodes vorzüglich scannen, interpretieren und das Ergebnis an den verwendeten Rechner, bzw. an die darauf ausgeführte Software weitergeben.
Durch Ausprobieren der mit einem Barcodeprogramm generierten Barcodes ist mir ebenfalls seit vielen Jahren bekannt, dass es sich bei den verwendeten Barcodes um Barcodes des Typs „2 of 5 interleaved“ handelt. Doch was bedeutet dieser Name eigentlich?
Wenn nun ein Barcode-Scanner mit der Intelligenz von ein bisschen Silizium in der Lage ist so einen Barcode zu decodieren, sollten doch 1446 Gramm bzw. 1330 Gramm menschlichen Gehirns dazu ebenfalls in der Lage sein? Und damit meine ich nicht, die unter dem Barcode abgedruckten Ziffern in Klartext abzulesen…
An der Stenkefelder Berufsschule [2] gibt es sogar ein Seminar, um Barcodes manuell zu lesen 🙂
Also los geht’s…
Zeichensatz
Mit „2 of 5 interleaved“ lässt sich nur ein numerischer Zeichensatz, d.h. die Zeichen 0 bis 9, abbilden.
Start- und Stopp-Zeichen
Erst einmal hat so ein Barcode ein Start- und ein Stopp-Zeichen, damit man weiß, wo vorne und wo hinten von dem Barcode ist.
Das Start-Zeichen sieht folgendermaßen aus: schmaler Balken, schmaler Zwischenraum, schmaler Balken, schmaler Zwischenraum.
Das Stopp-Zeichen sieht so aus: breiter Balken, schmaler Zwischenraum, schmaler Balken.
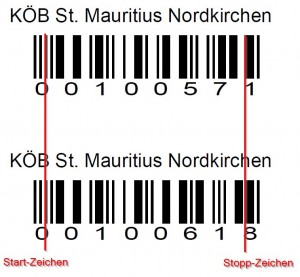
Abbildung 1: Abgrenzung der Start- und Stopp-Zeichen
Das Start- und das Stopp-Zeichen sind nach oben genannter Beschreibung in Abb. 1 außerhalb der roten Striche deutlich zu erkennen.
Zwischen den roten Strichen steht die Nutzinformation.
Barcodelänge
Barcodes des Typs „2 of 5 interleaved“ haben einschließlich der Prüfziffer (sofern verwendet), immer eine geradzahlige Länge.
Wenn die dargestellte Zahl das nicht hergibt, wird vorne mit Nullen aufgefüllt. Dies hat den Hintergrund, dass die zu zwei Ziffern gehörenden Striche jeweils in einander verschachtelt sind.
Ein Beispiel dazu:
Dargestellt werden soll die Zahl 321. Damit die Bedingung einer geradzahligen Länge erfüllt wird, muss also auf 0321 aufgefüllt werden.
Da in unserer Bücherei eine ausreichende Zahlenkapazität zur Verfügung gestellt werden sollte, hat man sich damals auf eine 8-stellige Länge geeinigt.
Die abzubildende Zahl muss also wie folgt aussehen: 00000321
Barcodeelemente
Die Elemente des Barcodes sind schwarze Balken und weißer Zwischenraum.
Die schwarzen Balken und die weißen Zwischenräume wechseln sich immer ab.
Die digitale Information (0 oder 1) ist in der Breite der schwarzen Balken bzw. der weißen Zwischenräume codiert.
Ein breites Element beinhaltet die Information „1“, ein schmales Element hingegen beinhaltet die Information „0“.
„Breite Elemente sind 2,0 bis 3,0 mal so breit wie schmale Elemente (bei Elementen kleiner 20mil [1mil = 1/1000 inches] ist der Faktor mindestens 2,2)“ [3]
Jedes Zeichen der im Barcode abgebildeten Zahl besteht aus fünf Elementen.
Daher die „5“ in „2 of 5 interleaved“
Stets sind zwei dieser fünf Elemente breit und drei sind schmal.
Interleaving (dt.: Verschachtelung)
Das „interleaved“ in „2 of 5 interleaved“ besagt, dass eine Verschachtelung Anwendung findet.
Da, wie oben bereits erwähnt, die zu zwei Ziffern gehörenden Striche ineinander verschachtelt sind, macht auch die „2“ in „2 of 5 interleaved“ Sinn.
Die zu zwei Ziffern gehörenden jeweils ineinander verschachtelten 10 Elemente, beinhalten folglich 4 breite und 6 schmale Elemente.
Das lässt sich an Abbildung 2 nachvollziehen.
Die erste Ziffer des Ziffernpaares ist in den schwarzen Strichen codiert („Strichcodierung“, im Beispiel Abb. 2: blaue Bits), die zweite Ziffer des Ziffernpaares ist in den weißen Zwischenräumen codiert („Lückencodierung“, im Beispiel Abb. 2: lila Bits).
Masterbeispiel
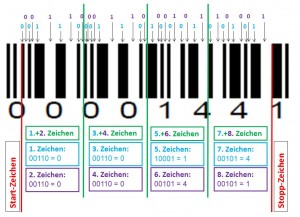
Abbildung 2: Masterbeispiel – Darstellung der Zahl: 00001441
Zeichensatz
Wie kommt man nun von den Einsen und Nullen, z.B. aus dem Beispiel in Abbildung 2, auf den codierten Dezimalwert?
| Ziffer | LSB | MSB | Parity | ||
| 1 | 2 | 4 | 8 | ||
| 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 1 |
| 8 | 1 | 0 | 0 | 1 | 0 |
| 9 | 0 | 1 | 0 | 1 | 0 |
Abbildung 3: Decodiertabelle, Quelle: [3]
Im Prinzip muss man nur die für ein Zeichen erhaltene Folge aus Einsen und Nullen in der Tabelle unter Abbildung 3 suchen (LSB bis MSB und Paritätsbit) und in die vorne stehende Ziffer übersetzen, z.B. ist „00101“ = 4.
Die Decodiertabelle habe ich unter zwei Quellen gefunden: [3] und [5].
Selbstverständlich handelt es sich um einen 2-aus-5-Code, was dem Anwendungszweck geschuldet ist. Weitergehende Informationen dazu habe ich nicht gefunden.
Wem weitere Informationen zum Code selbst vorliegen, möge mich bitte informieren.
Das Paritätsbit (letztes Bit) dient der Erkennung einer fehlerhaft gelesenen Information.
Das Paritätsbit hängt dem Informationswert, d.h. der Folge von Bits an.
Ist die Anzahl der mit 1 belegten Bits im Informationswort gerade, ist das Paritätsbit 0.
Ist die Anzahl der mit 1 belegten Bits im Informationswort ungerade, so ist das Paritätsbit 1.
Dieser Umstand lässt sich leicht an der Tabelle in Abbildung 3 nachprüfen.
„Die Methode der Fehlererkennung mittels Paritätsbits heißt Paritätsprüfung. Da nicht bekannt ist, wo innerhalb des Codewortes der Fehler aufgetreten ist, ist keine Fehlerkorrektur möglich.“ [6]
Es wird aber erkannt, dass die gelesene Information nicht plausibel ist. Somit wird eine als n.i.O. erkannte Information nicht an den Rechner weitergegeben.
Prüfzifferberechnung
Eine Prüfziffer lässt die Erkenntnis zu, ob der Barcode korrekt gelesen wurde.
Bei der Prüfziffer handelt es sich um die letzte Ziffer des Barcodes.
In unserer Bücherei sind die Barcodes durchgängig nummeriert, unterscheiden sich jedoch in der letzten Ziffer, da die letzte Ziffer die Prüfziffer ist.
Die Prüfziffer wird wie folgt berechnet:
„1. Die rechts außen stehende Ziffer bekommt Gewichtung 3. Dann nach links gehend abwechselnd die Gewichtungen 1, 3, 1, 3, 1, 3, etc vergeben.
2. Die Gewichtungen mit den Ziffern multiplizieren und Summe aller Ergebnisse bilden.
3. 10 – (Ergebnis Modulo 10) ermitteln“ [3]
Beispiel:
In Abbildung 2 steht der Wert 00001441 im Barcode.
Bei der letzten Ziffer handelt es sich um die Prüfziffer. Passt sie?
Wert 0000144
Wertigkeit 3131313
Multiplikation 3|4|12
Summe 3+4+12=19
Modulo bezeichnet den Rest einer Division
10 – (19 mod 10) = 10 – (9) = 1
Die Prüfziffer 1 stimmt also!
Weiterführende Informationen
Für weiterführende Informationen siehe Links unter den Quellen [3] bis [5].
Quellen und Links:
[1] Katholische öffentliche Bücherei St. Mauritius Nordkirchen
http://www.buecherei-nordkirchen.de
[2] Stenkefeld: Barcode
http://www.stenkelfeld.com/gewerbe/berufsschule/barcode.html
[3] Zentrale Datenbank HI-Tier (ZDB): Barcode „Interleaved 2 of 5“
https://www3.hi-tier.de/Entwicklung/Technik/barcode_i2of5.html
[4] Suchy MIPS
http://www.suchymips.de/de/barcode-2-5-interleaved.htm
[5] Strichcodeservice
http://www.strichcode.co.at/strichcodeservice/2aus5_interleaved.htm
[6] Paritätsbit
https://de.wikipedia.org/wiki/Parit%C3%A4tsbit
